トライボロジーによるブレーキパッドの評価
ブレークパッドの性能を評価することの重要性
ブレーキパッドは、複数の材料からなる複合材料であり、多くの安全要求を満足させることが必要です。理想的なブレーキパッドは、高い摩擦係数(COF)、低い摩耗率、最小限の騒音、そして様々な環境下で信頼性を維持することです。ブレーキパッドの品質がその要求を満たすことができるようにするために、トライボロジー試験は重要な仕様を特定するために使用することができます。
ブレーキパッドの信頼性の重要性は非常に高く、乗員の安全性を無視することは許されません。そのため、運転状態を再現し、故障の可能性がある箇所を特定することが重要です。
ナノベアを使うと トライボメータ、ピン、ボール、またはフラットと、常に移動する相手材との間に一定の荷重がかかります。 2 つの材料間の摩擦は硬いロードセルで収集されるため、さまざまな荷重と速度での材料特性の収集が可能になり、高温、腐食性、または液体環境でのテストが可能になります。
測定目的
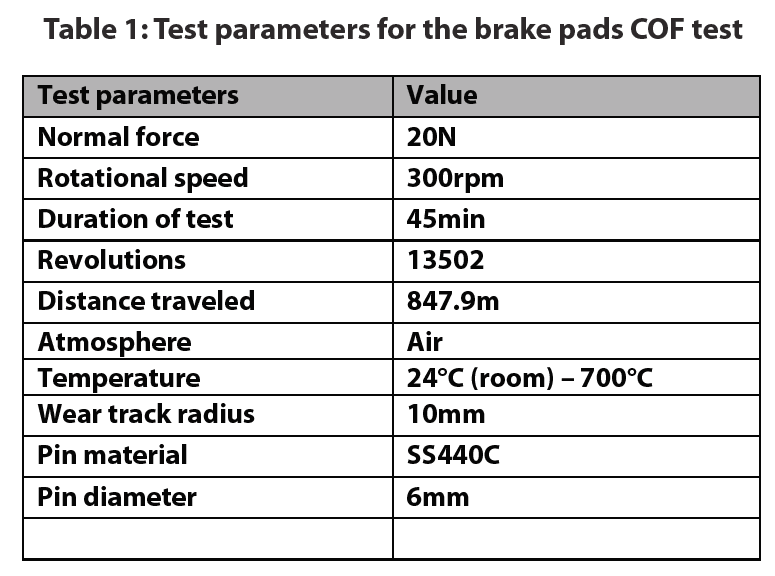
本研究では,室温から700℃まで連続的に温度上昇する環境下で,ブレーキパッドの摩擦係数を調査した。環境温度は、ブレーキパッドの顕著な破損が観察されるまでその場で上昇させた。摺動界面付近の温度を測定するために、ピンの裏側に熱電対を取り付けた。
結果および考察
この研究では、主にブレーキパッドが破損し始める温度に焦点を当てています。ピンの材質がブレーキローターと異なるため、得られたCOFは現実の値を表していない。また、収集した温度データはピンの温度であり、摺動界面温度ではないことに注意が必要である。
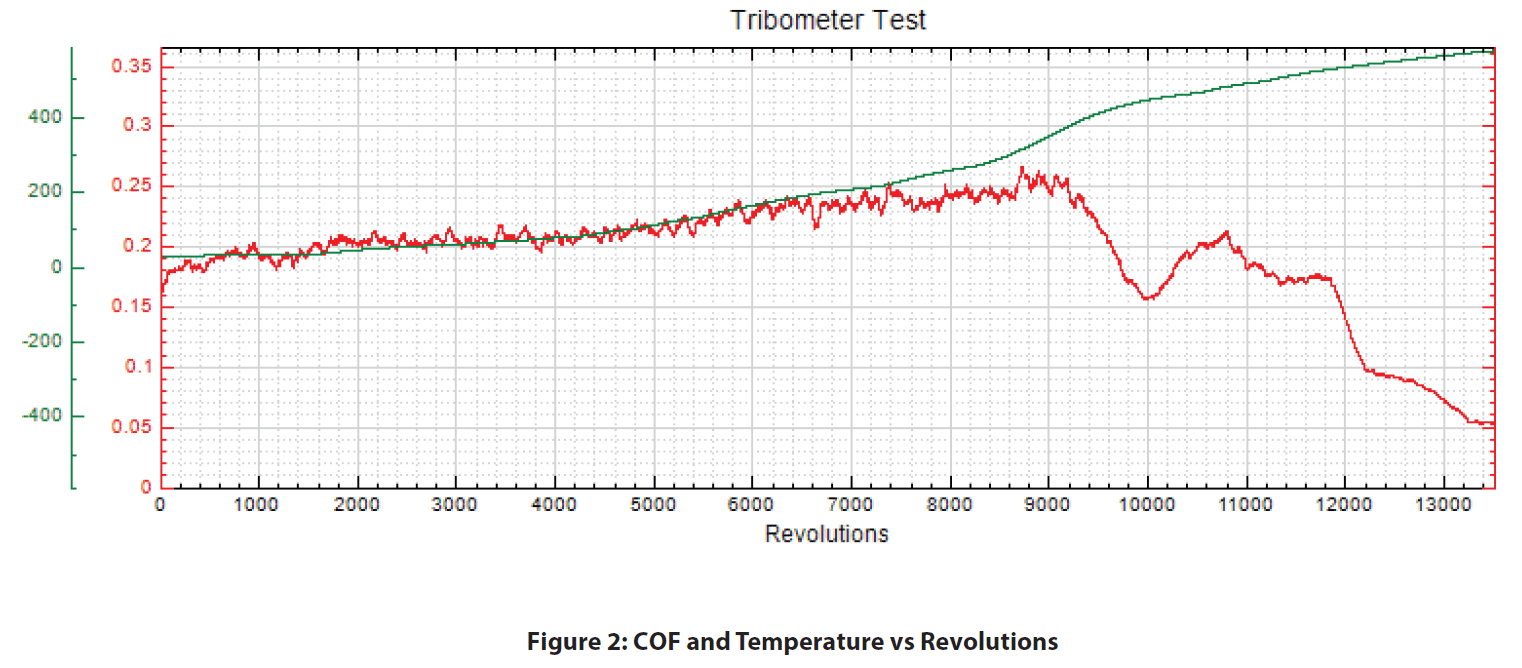
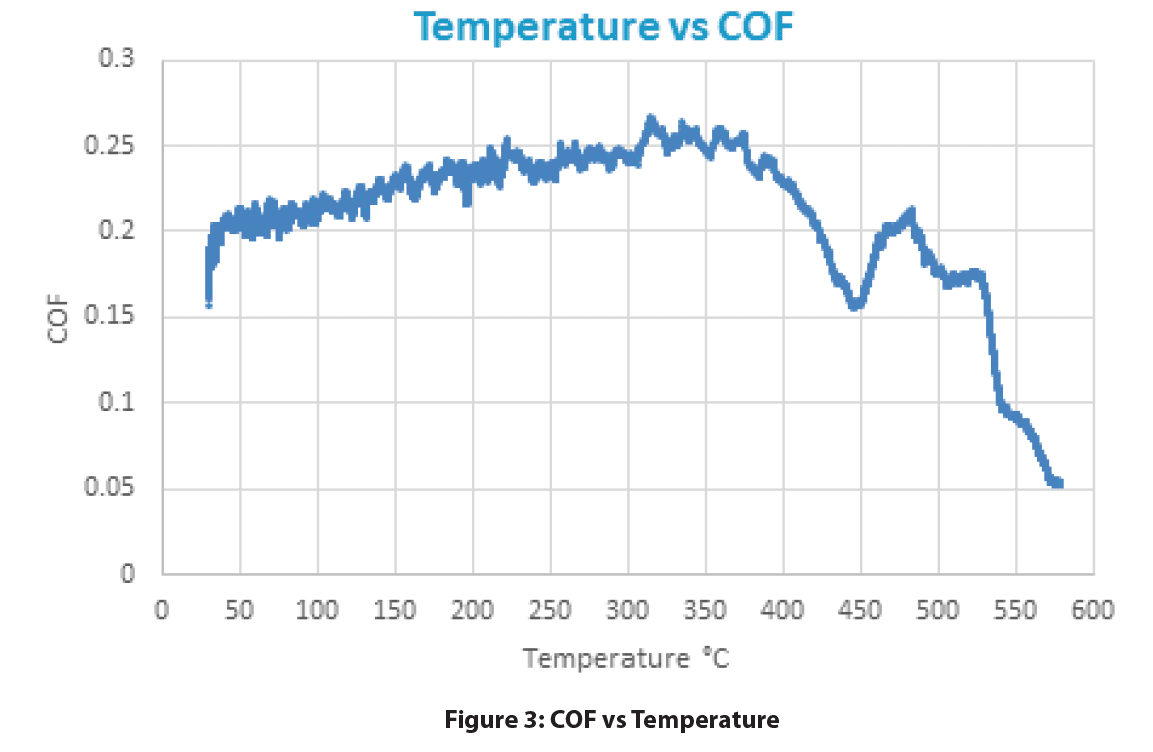
試験開始時(室温)、SS440CピンとブレーキパッドのCOFは約0.2の安定した値を示した。温度が上昇するにつれ、COFは着実に増加し、350℃付近で0.26の値でピークに達した。390℃を超えると、COFは急速に減少し始める。COFは450℃で0.2まで回復し始めたが、その直後に0.05まで減少し始めた。
ブレーキパッドが常に破損する温度は、500℃以上であることが確認された。この温度を過ぎると、COFはもはや出発時のCOFである0.2を維持することができなくなった。
結論

このブレーキパッドは、500℃を超える温度で一貫して破損を示しました。0.2だったCOFは0.26までゆっくりと上昇し、試験終了時(580℃)には0.05まで低下しています。0.05と0.2の差は4倍。つまり、同じ制動力を得るためには、580℃では常温の4倍もの法線力が必要なのです
この研究には含まれていませんが、ナノベーストライボメータは、ブレーキパッドのもう一つの重要な特性である摩耗速度を観察するための試験も行うことが可能です。当社の3D非接触型プロフィロメータを利用することで、摩耗痕の体積を取得し、サンプルの摩耗速度を算出することができます。ナノベーストライボメータは、さまざまな試験条件や環境下で摩耗試験を行うことができ、使用条件を最もよく再現することができます。
さて、次はアプリケーションについてです。
カテゴリー
- アプリケーションノート
- ブロック・オン・リングトライボロジー
- 腐食トライボロジー
- 摩擦試験|摩擦係数
- 高温機械試験
- 高温トライボロジー
- 湿度・ガス トライボロジー
- 湿度機械試験
- 圧痕|クリープとリラクゼーション
- 圧痕|破壊靭性
- 圧痕|硬度・弾性率
- 圧痕|紛失と保管
- 圧痕|応力と歪み
- 圧痕|降伏強度と疲労の関係
- ラボラトリーテスト
- リニアトライボロジー
- 液体機械試験
- 液状トライボロジー
- 低温トライボロジー
- メカニカルテスト
- プレスリリース
- プロフィロメトリー|平坦度・反り率
- プロフィロメトリー|幾何学と形状
- プロフィロメトリー|粗さと仕上がり
- プロフィロメトリー|段差の高さと厚み
- プロフィロメトリー|テクスチャーとグレーン
- プロフィロメトリー|体積・面積
- プロフィロメトリーテスト
- リング・オン・リング トライボロジー
- 回転トライボロジー
- スクラッチテスト|接着剤の不具合について
- スクラッチテスト|コヒーシブフェール
- スクラッチテスト|マルチパス摩耗
- スクラッチテスト|スクラッチハードネス
- スクラッチテスト トライボロジー
- トレードショー
- トライボロジー試験
- 未分類
月別アーカイブ
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月