
表面境界測定
3Dプロフィロメトリーによる表面境界計測
詳細はこちら
表層境界測定
3Dプロフィロメトリーによる

作成者
クレイグ・ライジング
はじめに
表面の特徴、パターン、形状などの界面が配向性を評価されるような研究では、測定プロファイル全体にわたって関心のある領域をすばやく特定することが有用です。表面を重要な領域に分割することで、ユーザーは境界、ピーク、ピット、面積、体積などを迅速に評価し、研究対象の表面プロファイル全体における機能的な役割を理解することができます。例えば、金属の粒界イメージングでは、多くの構造物の界面や全体的な方向性が解析の重要なポイントになります。それぞれの領域を理解することで、全体の中の欠陥や異常を特定することができます。粒界のイメージングは通常プロフィロメータの能力を超える領域で研究され、2D画像分析に過ぎませんが、3D表面測定の利点とともに、ここで紹介する概念をより大きなスケールで説明するための参考資料となります。
表面分離研究における3次元非接触形状測定機の重要性
タッチプローブや干渉計などの他の技術とは異なり、 3D非接触形状計軸色収差を使用するため、ほぼすべての表面を測定でき、オープンステージングによりサンプルサイズは大きく変化する可能性があり、サンプルの前処理は必要ありません。ナノからマクロの範囲は、サンプルの反射率や吸収の影響を受けずに表面プロファイル測定中に得られ、高い表面角度を測定する高度な機能を備えており、結果をソフトウェアで操作する必要はありません。透明、不透明、鏡面、拡散、研磨、粗いなど、あらゆる材質を簡単に測定できます。非接触粗面計の技術は、表面境界分析が必要な場合に表面調査を最大限に高めるための理想的で広範で使いやすい機能を提供します。 2D と 3D 機能を組み合わせたメリットも得られます。

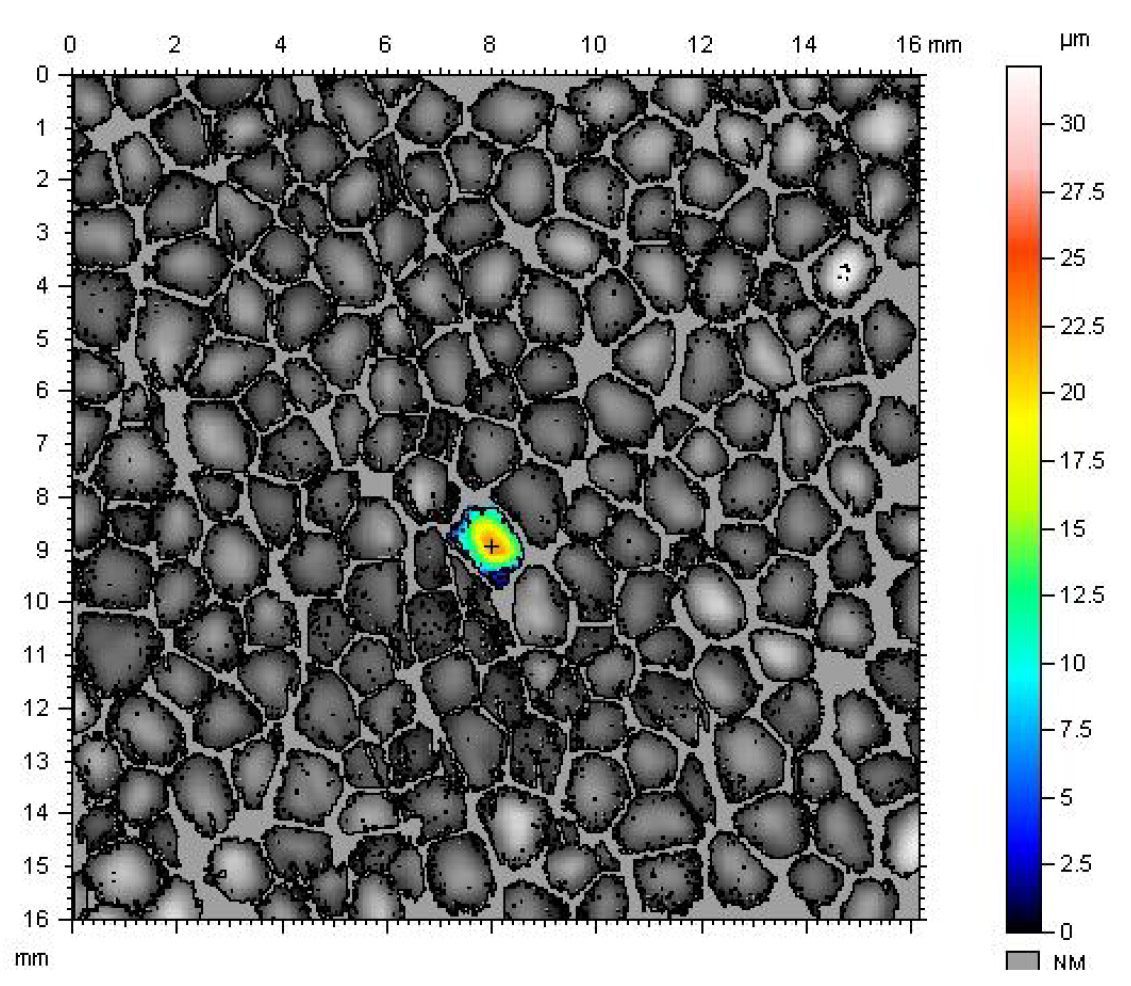
トポグラフィー画像(左下)を反射強度画像(右下)でマスクし、結晶粒の境界を明確にした画像。直径565μm以下の粒はフィルターをかけることで無視されている。


粒の総数167
粒が占める投影面積の合計。166.917 mm² (64.5962 %)
バウンダリー占有予想総面積: (35.4038 %)
粒の密度0.646285粒/mm2
外周=9114.15μm +/- 4570.38μm
等価直径 = 1098.61 µm +/- 256.235 µm
平均直径 = 945.373 µm +/- 248.344 µm
最小径 = 675.898 µm +/- 246.850 µm
最大径=1312.43 µm +/- 295.258 µm
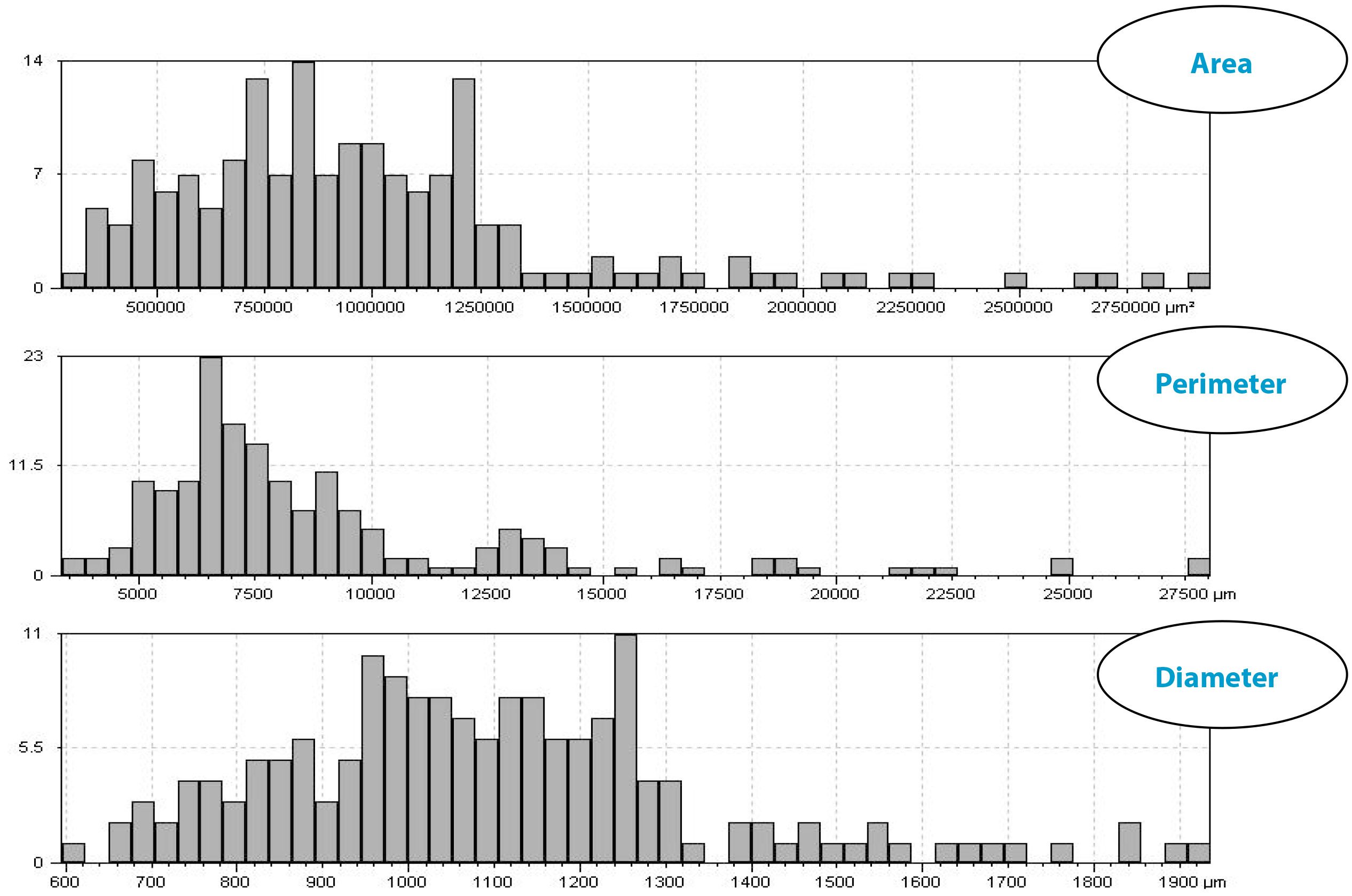
結果&考察:3次元表面境界計測
得られた3次元トポグラフィーデータを用いて、各粒子の体積、高さ、ピーク、アスペクト比、一般的な形状情報を解析することができる。3次元占有総面積:2.525mm3
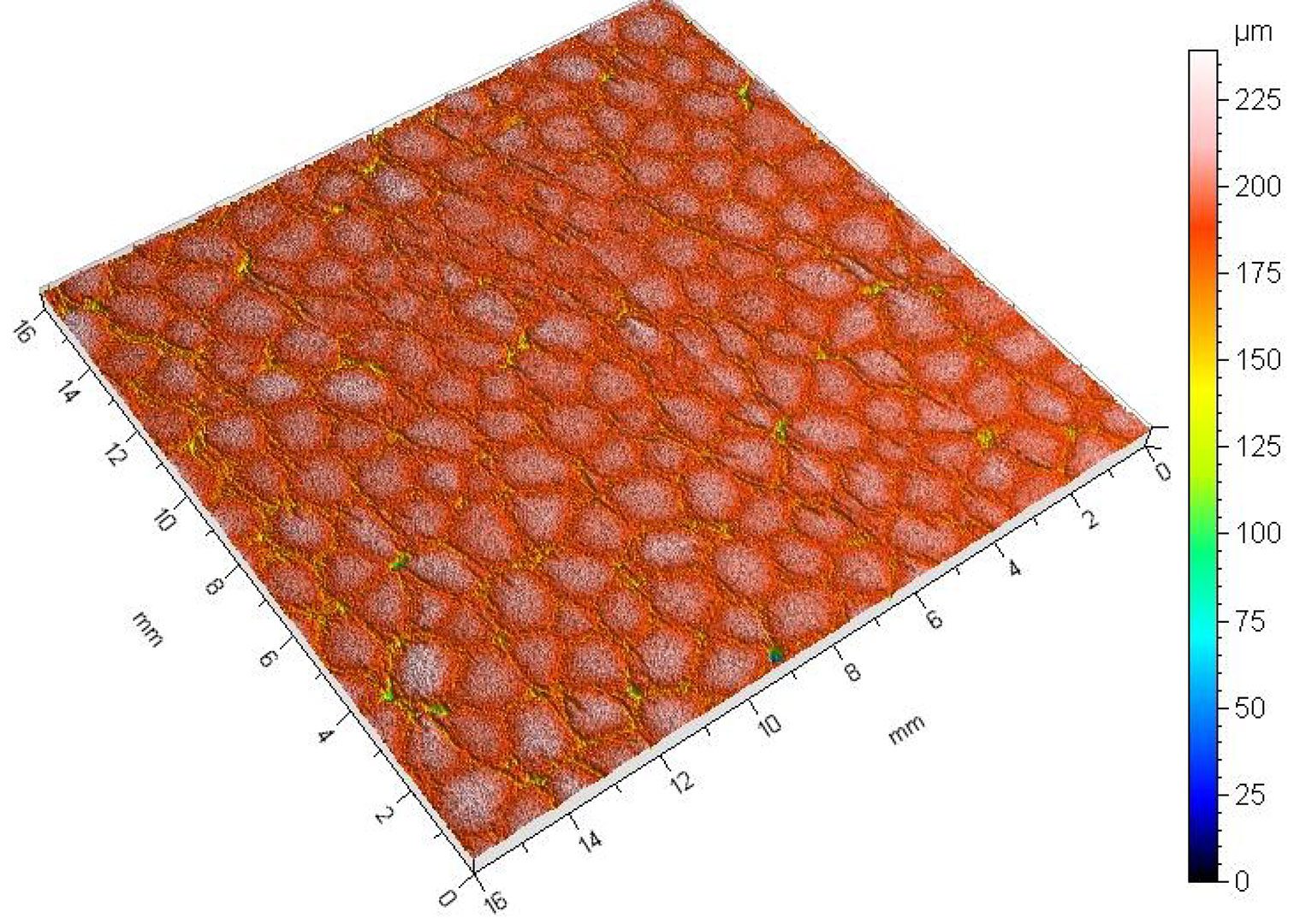
まとめ
このアプリケーションでは、NANOVEA 3D非接触形状測定機が発泡スチロールの表面を精密に特性評価できることを示しました。統計的な情報は、表面全体、またはピークやピットなどの個々の粒子について得ることができます。この例では、ユーザーが定義したサイズより大きいすべての粒を使用して、面積、周囲長、直径、高さを表示しました。ここで示された特徴は、バイオメディカルからマイクロマシニングまで、様々な分野の自然表面や加工済み表面の研究および品質管理に重要な役割を果たすことができます。
さて、次はアプリケーションについてです。
カテゴリー
- アプリケーションノート
- ブロック・オン・リングトライボロジー
- 腐食トライボロジー
- 摩擦試験|摩擦係数
- 高温機械試験
- 高温トライボロジー
- 湿度・ガス トライボロジー
- 湿度機械試験
- 圧痕|クリープとリラクゼーション
- 圧痕|破壊靭性
- 圧痕|硬度・弾性率
- 圧痕|紛失と保管
- 圧痕|応力と歪み
- 圧痕|降伏強度と疲労の関係
- ラボラトリーテスト
- リニアトライボロジー
- 液体機械試験
- 液状トライボロジー
- 低温トライボロジー
- メカニカルテスト
- プレスリリース
- プロフィロメトリー|平坦度・反り率
- プロフィロメトリー|幾何学と形状
- プロフィロメトリー|粗さと仕上がり
- プロフィロメトリー|段差の高さと厚み
- プロフィロメトリー|テクスチャーとグレーン
- プロフィロメトリー|体積・面積
- プロフィロメトリーテスト
- リング・オン・リング トライボロジー
- 回転トライボロジー
- スクラッチテスト|接着剤の不具合について
- スクラッチテスト|コヒーシブフェール
- スクラッチテスト|マルチパス摩耗
- スクラッチテスト|スクラッチハードネス
- スクラッチテスト トライボロジー
- トレードショー
- トライボロジー試験
- 未分類
月別アーカイブ
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月
- 2022年7月










